Recursive functions in Power Query

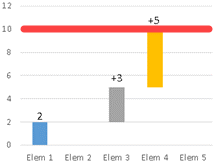
In Power Query there are no loops. There are no "For each", "For next", "Do Until" blocks. In Power Query we can accomplish the same thing with recursive functions. Let's say that we want to sum elements of a list, from the start, until our sum reach 10 or more. Question is, after how many elements, our goal will be reached. We can see on the chart that our goal will be reached after 4-th element 2 + 0 + 3 + 5 = 10.

First we have to establish our initial state. We know that our list is { 2,0,3,5,0 } and that initial sum is zero. We also know that first element in the list has index zero. We can write that into query. This query will call recursive function which will supply the final result.

let 
	List = { 2,0,3,5,0 }
	, Sum = 0
	, ElementIndex = 0
	, NoOfElements = RecursiveFunction ( List, Sum, ElementIndex )
in
	NoOfElements

Second, what is our logic? Our logic will go like this:
0) Does our initial state (Sum=0) meet the condition? It doesn't, so we'll go to next step.
1) We'll add one element to sum. We got 2, this doesn't meet the condition so we go to next step.
2) We'll add another element to sum. We got 2 (2+0), this doesn't meet the condition so we go to next step.
3) We'll add another element to sum. We got 5 (2+3), this doesn't meet the condition so we go to next step.
4) We'll add another element to sum. We got 10 (5+5), this does meet the condition so our answer is 4 elements.

Step 0) is already described in our query. Steps 1-4 are pretty similar. They have the same logic, but initial state for each step is different. All we have to do is to wrap this logic into function and then to call that function with different arguments each time.  Our recursive function is bellow. If condition is satisfied, we will return "Sum", otherwise we will call function again, this time with different arguments. That will repeat until condition is met.

( List, Sum, ElementIndex ) => 
let
  SubTotal = if Sum >= 10 then Sum else
    RecursiveFunction( List, Sum + List{ ElementIndex }, ElementIndex + 1)
in
    SubTotal

Every recursive function has the same logic. First we establish initial state and then we repeat this two steps until condition is met:
– Does current state satisfied the condition? If does, then we have final result.
– If it doesn't, we'll change the state and new state will give as arguments for another call of function itself.

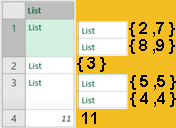
Let's do one more complex example. Now we have a bunch of nested lists. Our goal is to sum all scalar values in those lists. Our condition is that we use all scalar values, so we are looking for the sum of 2 + 7 + 8 + 9 + 3 + 5 + 5 + 4 + 4 + 11 = 58.

First, we will establish initial state. We know that initial sum is zero, and we have our list. This query will call recursive function which will supply final result.

let 
          NestedLists = {  { { 2, 7 }, { 8, 9 }  }
                         , { 3 }
                         , { { 5, 5 }, { 4, 4 } }   	
                         , 11
          }
        , Sum = 0
        , ElementIndex = 0
	, Total = NestedListsRecursiveFunction ( NestedLists, Sum, ElementIndex )
in
	Total

All we need more is a recursive function. This function is complex. Let's try to make it easier to understand by thinking about simplier NestedLists = { 1, { 2 }, 2, { 3 } }. We can present this list by picture:

First we will count how many toothbrushes are in each package. After that is easy to sum the whole list.

Here is the trick. Addition of all toothbrushes in one package is similar to addition of all toothbrushes in the whole list. This mean that we can use same logic to individual package and to whole list. That means we can use recursion. Here is recursion function.

(NestedLists, Sum, ElementIndex) =>
  let
    NewSum = 
      if ElementIndex < List.Count(NestedLists) then
        if Value.Is(NestedLists{ElementIndex}, List.Type) then
          NestedListsRecursiveFunction(
              NestedLists 
            , Sum + NestedListsRecursiveFunction(NestedLists{ElementIndex}, 0, 0) 
            , ElementIndex + 1
          )
        else
          NestedListsRecursiveFunction(
              NestedLists 
            , Sum + NestedLists{ElementIndex} 
            , ElementIndex + 1
          )
      else
        Sum
  in
    NewSum

With purple code we are passing through all elements of a List. If we reach the final element, function will return sum of that List as final result. For each element we are using red code to determin if element is List or not.  If element is scalar, we will use green line above to add such element. Problem is that beside scalar elements, we can also have subList elements.

Orange code is used to add such elements. It is similar to green code. Green code is adding scalar values, and orange code is adding sums of subLists. Blue code above is used to sum every subList. Blue code is using recursion.

So this is our goal, we want to replace every subList with its sum. When we reach subList element, we will dive in it with recursive call to the function. If that subList element has only scalars, green line of code will give us sum of that subList. If that is not true, we will dive deeper until we find subList that contains only scalars. When we get sums of lowest subLists, we can use those to calculate sums for subLists that are higher in hierarchy.

Excel file with sample in Power Query: