0210 Aggregate Functions and Logical Functions

MonetDB / By / November 10, 2025

Aggregation Functions

Sample Table for Aggregation Functions

CREATE TABLE aggtable( Number INT, Word VARCHAR(8), intervalMonth INTERVAL MONTH );

INSERT INTO aggtable( Number, Word, intervalMonth )
VALUES  ( 2, 'two', INTERVAL '2' month ), ( 2, 'two', INTERVAL '2' month )
            , ( 3, 'three', INTERVAL '3' month ), ( 4,'four', INTERVAL '6' month )
            , ( NULL, NULL, NULL );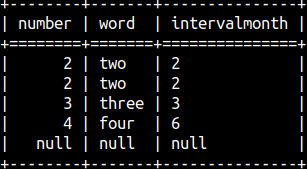

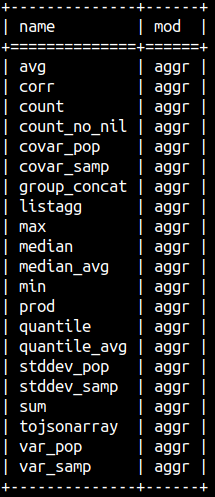
Sys.Functions System Table

We can get a list of aggregate functions from the system table sys.functions. Aggregate functions are of the type 3.  

SELECT DISTINCT name, mod FROM sys.functions WHERE type = 3 ORDER BY name;  

We can divide aggregate functions into three groups:

Arithmetic functionsConcatenation functionsStatistic functions
avg,
count, count_no_nil,
max, min,
prod,
sum		group_concat,
listagg,
tojsonarray		corr,
covar_pop, covar_samp,
median, median_avg,
quantile, quantile_avg,
stdev_pop, stdev_samp,
var_pop, var_samp

Arithmetic Functions

SQLResultCalculationComment
SELECT AVG( Number ) FROM aggTable;2.75(2+2+3+4)/4 = 2.75NULL is ignored.
SELECT COUNT( * ) FROM aggTable;5Count the rows of the table. 
SELECT COUNT( Word ) FROM aggTable;4Count words, without NULL. 
SELECT COUNT_NO_NIL( Word ) FROM aggTable;Error Doesn't work.
SELECT MAX( Word ) FROM aggTable;'two'Last value.Words are ordered alphabetically, A-Z.
SELECT MIN( Number ) FROM aggTable;2First value.Numbers are ordered numerically.
SELECT PROD( Number ) FROM aggTable;482*2*3*4=48 
SELECT SUM( Number ) FROM aggTable;112+2+3+4=11 
SELECT SUM( intervalMonth ) FROM aggTable;132+2+3+6=13Also work with seconds. Result is of interval type.

We can use DISTINCT keyword to exclude duplicates. In our sample table, only number 2 is duplicate. Calculations below will be done like that duplicate value doesn't exist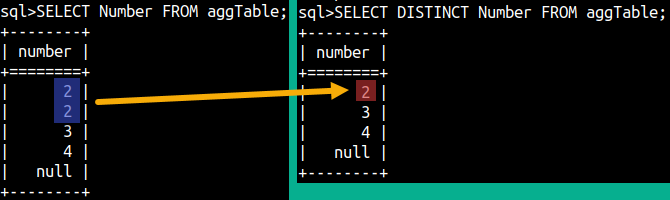

SQLResultCalculation
SELECT AVG( DISTINCT Number ) FROM aggTable;3(    2    +3+4)/3 = 3
SELECT COUNT( DISTINCT Word ) FROM aggTable;3Count words, no NULLs, no duplicates.
SELECT PROD( DISTINCT Number ) FROM aggTable;24     2     *3*4 = 24
SELECT SUM( DISTINCT Number ) FROM aggTable;9      2     +3+4 = 9
SELECT SUM( DISTINCT  intervalMonth ) FROM aggTable;9     2     +3+4 = 9

Concatenation Functions

Concatenation is a way to aggregate text. Instead of having text occupying N rows, where on each row we have only one phrase, we can aggregate them all into one row.
Result will be comma separated list of those phrases, although we can choose what delimiter will be used instead of the comma.

If we want to remove duplicates, we have to use DISTINCT keyword before the name of a column.

Null values will be ignored.

SQLResultComment
SELECT LISTAGG( Word, '|' ) FROM aggTable;two|two|three|fourDefault delimiter is a comma. Returns VARCHAR.
SELECT LISTAGG( DISTINCT Word, '|' ) FROM aggTable;two|three|fourWith the DISTINCT we can remove duplicates.
SELECT SYS.GROUP_CONCAT( Word, ';' ) FROM aggTable;two;two;three;fourDefault delimiter is a comma. Returns CLOB.
SELECT JSON.ToJsonArray( Word ) FROM aggTable;[ "two","two","three","four" ]Result is JSON list.
SELECT JSON.ToJsonArray( Number ) FROM aggTable;[ "2", "2","3","4" ]Works with numbers, too.

SELECT LISTAGG( Word ORDER BY Number ) FROM aggTable;two,two,three,fourWe can control the order of the elements.
SELECT SYS.GROUP_CONCAT( Word, '+' ORDER BY Number DESC ) FROM aggTable;four+three+two+twoWe can control order and the separator.

When we use ORDER BY with the concatenation functions, then it is not possible to use DISTINCT keyword.

Statistical Functions

Numbers, from Number column, can be divided into smaller and larger numbers. Half of the numbers will be smaller and the other half will be larger numbers. The number on the border between the smaller and larger numbers is the median.

SQLResultResult if we add number 5 to our column.
SELECT SYS.MEDIAN( Number ) FROM aggTable;21,2(2),33,44         =>      221,22,3(3),44,55         =>     3
SELECT SYS.MEDIAN_AVG( Number ) FROM aggTable;21,2(2),3(3),44         =>       (2+3)/2 = 2.521,22,3(3),44,55         =>     3

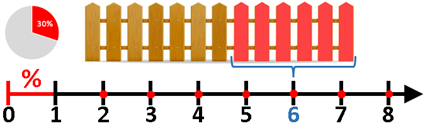
Median is a special case of a quantile. Median is a 50% quantile. But we can differently divide our numbers. We can divide them 60% vs 40%, so that 60% numbers are on the smaller side, and 40% is on the bigger side. Number between them would be called 60% quantile. In our example below, "60 % quantile" is 2.8, which means that 60% of numbers is below 2.8. This would be more obvious if we had more numbers in our column.

SQLResultCalculation
SELECT SYS.QUANTILE_AVG( Number, 0.6 ) FROM aggTable;2.8( 4 – 1 ) * 0.6 + 1, where 4 is the count of our numbers.
SELECT SYS.QUANTILE( Number, 0.6 ) FROM aggTable;3This is just value from above, rounded to integer.

Variance and standard deviation are calculated differently depending whether our data represent a population or a sample.

SQLResultCalculation 
SELECT SYS.VAR_SAMP( Number ) FROM aggTable;0.917
SELECT SYS.StdDev_SAMP( Number ) FROM aggTable;0.957sqrt( variance ) = sqrt( 0.917 ) = 0.957
SELECT SYS.VAR_POP( Number ) FROM aggTable;0.687
SELECT SYS.StdDev_POP( Number ) FROM aggTable;0.829sqrt( variance ) = sqrt( 0.687 ) = 0.829

Covariance in statistics measures the extent to which two variables vary linearly.  Correlation is just covariance measured in normalized units.

SQLResult in MonetDBCalculation 
SELECT SYS.COVAR_SAMP( Number, 10 - Number * 1.2 ) FROM aggTable;-1.1
SELECT SYS.COVAR_POP( Number, 10 - Number * 1.2 ) FROM aggTable;-0.825
SELECT SYS.CORR( Number, 10 - Number * 1.2 ) FROM aggTable;-1

All statistic function will ignore NULLs.

Logical Operators

Binary Operators

SQLResultComment
SELECT True AND True;TRUEReturns TRUE only if both arguments are TRUE.
SELECT True OR False;TRUEReturns TRUE if at least one argument is TRUE.

Unary Operators

SQLResultComment
SELECT NOT True;FALSEWill transform TRUE to FALSE, and FALSE to TRUE. Always the opposite.
SELECT Null IS NULL;TRUEChecks whether something is NULL.
SELECT Null IS NOT NULL;FALSEChecks whether something is NOT NULL.

All other logical operators will return Null if at least one of its arguments is Null.

SQLResult
SELECT NOT Null;NULL
SELECT Null AND True;NULL

Most SQL functions will either return NULL if one of the arguments is NULL, or will ignore rows with NULL values.

Logical Functions

Operators AND, OR and NOT have alternative syntax where they work like functions.  XOR can not work like operator, only like a function.

SQLResultComment
SELECT "xor"(True, False);TRUEReturns TRUE only when the first argument is the opposite of the second argument (Arg1 = NOT Arg2).
SELECT "and"(True, False);FALSEReturns TRUE only if both arguments are TRUE.
SELECT "or"(False, False);FALSEReturns TRUE if at least one argument is TRUE.
SELECT "not"(False);TRUEWill transform TRUE to FALSE, and FALSE to TRUE. Always the opposite.

0200 MonetDB: Window Functions Theory

MonetDB / By / November 11, 2025

Imagine people scattered through some area, looking through binoculars. None of them will see the whole scenery, they will only see part of it. It is like each of them is looking through the different window.

Now, imagine that in each row, of a database table, there is a data scientist looking through binoculars. Each data scientist can only see some of the rows from that table. Each data scientist has his own window.

What would scientist do to represent nature of data he is looking at? He would aggregate them. If each of our scientist decide to calculate average of data he is looking at, we would get a table like this one:

In the real database table, with millions of rows, these average values would not be representatives of anything. Our windows are too random. If we can create a rule by which windows are created, then we would have a scientific view of our data. Let's say that each data scientist can only see his own row, and previous two rows. Then we would have a rule. Check out animated image below (left image).

By using this rule for a window creation, we can calculate "moving averages", which are often used in statistics.

We can also define these rules in SQL if we use Window Functions. Window Functions are special, because they can define windows and then apply some aggregation to data in those windows. We can apply aggregations like SUM, AVG, MAX, but we can also use some special aggregation functions.

Window functions are also called Analytic functions, because they give us abilities that are beyond traditional SQL statements. With them we can do things which were previously hard to achieve in SQL, and they are really useful for a deep analysis of our data. Windows are like overlapping samples from our tables. They can reveal us how the nature of our data is changing through time and dimensions.

Terminology

In SQL, window, as explained above, is actually called "frame". The term "window" means something else. We will now discern difference between window, partition and a frame.

Frame is group of records that will be aggregated. Frame is presented with the moving red rectangle in the animation bellow.

Tables in animation below, show how many points each country won on some sport competition.

Sport results presented on the animation above will not be held in a database like three tables, but they will be placed together into one big table.  

That big table is our Window (assuming we are using no filters on that table).
Smaller tables are called Partitions.
Red moving rectangles are Frames.  

Window functions can process partitions separately, the same as they were separate tables.  

How to Define Window?

SELECT employee_id, salary
FROM employees
WHERE department_id = 101  
AND salary > (SELECT AVG(salary)                 FROM employees);		Subquery is not under direct influence of the outer query. In the example, we have a filter
department_id = 101 on the outer query. But subquery is not under the influence of that filter.
Subquery will calculate average salary for all of the employees. Meaning is, that we are looking for employees from department 101, that have bigger salary then the global average.

This is not true for window functions. Window is under influence of the query context. Everything that is used inside FROM, WHERE, GROUP BY and HAVING clauses will define our window. Window functions can only do their magic after the final dataset is defined and unchangeable. That also means that Window functions can only be used in SELECT and ORDER BY clauses.

How to Define Partitions?

Partitions can be defined by the values of one column. All rows that have the same value will be the same partition. On our image, all the rows with letter "A" will create Partition 1. It is also possible to use combination of the values from two or more columns to define partitions. Each unique combination of values will define a partition. On the image below, combination of values A and Q will define Partition 2. We can use expression to calculate values for our column(s). In our example, all the rows, where MOD function returns 1 will belong to Partition 1. Rows that return 0 will belong to Partition 2.

How to Define Frames?

Frames are moving and so, they are always calculated relative to the current row. Two other reference points are the first and the last row in our partition. Position of the frame is always relative to those reference points.

For definition of a frame, we have to define its start row, and its end row. End row has to be after Star row. Below we can see all the ways how to define start and end row.

                    Can only be START ROW
– UNBOUNDED PRECEDING – the first row in the partition                      
                    Can be both START or END ROW
– N PRECEDING – row that is N rows before current row.
– CURRENT ROW – our major reference point.
– M FOLLOWING – row that is M rows after current row.

                     Can only be END ROW
– UNBOUNDED FOLLOWING – the last row in the partition		An example:

Notice that for all of this to make sense, records have to be sorted.

What is a Group?

For window functions, start and end of a frame doesn't have to be a row. Start and end can also be defined with ranges and groups. Ranges and Groups are not individual records, they are sets of records.

Groups are defined similar to Partitions. All rows with the same value will be one group.

On the image to the left, current row is the row 5, but the current group is the Group 3. We are no more looking at 9 records, we are looking at 5 groups.

Our frame will start with one of the groups and will end with one of the groups after.		In this example, our frame will start with the first group in Partition, and will end on the group that is just after the current group.

What is a Range?

Relative positions are important for rows and groups, but not for ranges. With ranges, we are dealing with values in our column.

Let's say that some student took a school test. She scored 85 points on a test and she got a grade "A", because if number of points is between 76-100, then the grade is "A". It is similar with Ranges in window functions. Each frame is defined with a range of values. If a field value belongs to that range, then that record belongs to a frame defined by that range.

So, how we define a range? Really simple. If our current row has a value of X, we will add or subtract some number to that X, and we will get an extreme value of our range.

current value – N         
(syntax: N preceding)
                                          
current value + M        
(syntax: M following)		If, adjacent rows of the current row, have values that are close enough to the current value, then those rows will together make a frame.

Our frame is between [20,30], so all the rows beside the first and the last one, belong to this frame.  

Demonstration

This is a simple example of a window function. This example shows how to calculate cumulative of the qty column. We are not using PARTITION BY clause, so the whole table is one big partition.

0190 Common Table Expressions (CTE) in MonetDB

MonetDB / By / November 9, 2025

Table with billion rows and 100 columns, can be represented with one short name. We can use the same logic and give a name to our SELECT statements. If we want to use those SELECT statements in a subquery, join or union, we can refer to them by their names. This is how we can reduce any complex statement to its building blocks. This will break complex logic to simple steps, where each step is easy to understand and manage.

CTEs are a way to name our SELECT statement, and then to use those names in the final SELECT, INSERT, DELETE , UPDATE or MERGE statement.

Syntax of Common Table Expression

Bellow we can see statement with two CTEs. We can have them as many as we want ( Name1, Name2, Name3, Name4 … ). Each CTE will give a custom name to some SELECT statement. Thanks to this, final statement (which can be SELECT, INSERT, DELETE, UPDATE, MERGE), will be short and simple.

WITH
Name1 AS ( SELECT * FROM Table1 ),            --first CTE
Name2 AS ( SELECT * FROM Table2 )             --second CTE  
SELECT *                                      --final statement
FROM Name1   
       JOIN Name2 ON someCondition                  
       JOIN Name2 ON someOtherCondition;          

Not only CTE can break our logic into manageable elements, but it can also reduce repetition. We can write "SELECT * FROM Table2" once and then use it twice in the final statement. CTE will only improve readability of our statement and it will make it more concise. It will not improve performance of a statement.

Sample Tables

We will create two sample tables to use them in our CTEs.

CREATE TABLE Cte1 ( Letter CHAR, Number INTEGER );
INSERT INTO Cte1 ( Letter, Number ) VALUES ( 'A', 1 ), ( 'B', 2 );

CREATE TABLE Cte2 ( Letter CHAR, Number INTEGER );
INSERT INTO Cte2 ( Letter, Number ) VALUES ( 'P', 1 ), ( 'Q', 2 );     

Example with SELECT

WITH
Name1 AS ( SELECT * FROM Cte1 ),
Name2 AS ( SELECT * FROM Cte2 )
SELECT * FROM Name1
UNION
SELECT * FROM Name2;

Example with INSERT

WITH
Name1 AS ( SELECT * FROM Cte1 ),
Name2 AS ( SELECT * FROM Cte2 )
INSERT INTO Cte2
SELECT * FROM Name1
EXCEPT
SELECT * FROM Name2;		Because two tables don't have equal rows,
EXCEPT will return all the rows from the Cte1 table.

We will use CTE to insert those rows into Cte2.

Example with DELETE

WITH
Name1 AS ( SELECT Letter FROM Cte1 )
DELETE FROM Cte2
WHERE Letter   
      IN ( SELECT * FROM Name1 );                                    		When we use DELETE, we always have to delete from the table ( DELETE FROM Cte2 ). It is not possible to create a CTE, and then to delete from that CTE, like "DELETE FROM Name1", expecting that server will delete from the underlining table. That means that we only can use CTE in the WHERE clause.

After deleting A1 and B2 from Cte2, our Cte2 table is back to its original state.

Example with UPDATE

WITH
Name1 AS ( SELECT Number FROM Cte1 )
UPDATE Cte2
SET Letter = 'X'
WHERE Number   
   IN ( SELECT * FROM Name1 );		We will update all the letters in the table Cte2 where numbers are common for the both tables.
Because both tables have numbers 1 and 2, that means that all the letters in the table Cte2 will be updated to "X".

Again, CTE can only be used in the WHERE clause.

Example with MERGE

WITH
Name2 AS ( SELECT * FROM Cte2 )
MERGE INTO Cte1
USING Name2
ON Cte1.Letter = Name2.Letter
WHEN NOT MATCHED THEN INSERT ( Letter, Number )                                             VALUES ( Name2.Letter, Name2.Number );  		In MERGE statement, we can use CTE in the USING clause. Values from that CTE can be used to change values in the database table.

Our tables, Cte1 and Cte2 don't have common letters, so we don't have matches. That means that all the rows from our Cte2 table will be inserted into Cte1.

Aliases

We can use CTE without providing aliases to its columns.

WITH
Name1 AS ( SELECT * FROM Cte1 )
SELECT * FROM Name1;

If we want to, we can provide aliases in the SELECT statement. It is also possible to provide aliases after the name of the CTE. If both are provided, then the outside aliases will prevail ( Column1 and Column2, and not colLetter and colNumber ).

WITH
Name1 ( Column1, Column2 ) AS
( SELECT Letter AS colLetter, Number AS colNumber FROM Cte1 )
SELECT * FROM Name1;

Nested CTEs

WITH
Name1 AS ( SELECT * FROM Cte1 ),
Name2 AS ( SELECT * FROM Name1 )
SELECT * FROM Name2;		It is possible to reference one CTE from another CTE (Name2 is calling Name1 ).

WITH
Name1 AS ( SELECT * FROM Name2 ),
Name2 AS ( SELECT * FROM Cte2 )
SELECT * FROM Name2;		With nesting, we must be sure that referenced CTE is already defined. If we reference some
of the latter CTEs, then those CTEs will not be recognize ( Name1 cannot call Name2,
because it is not already defined ).

ORDER BY

In MonetDB, it is possible to use ORDER BY inside of CTEs definitions. That sorting will propagate to the final result.

WITH
Name1 AS ( SELECT * FROM Cte1 ORDER BY Letter DESC ),
Name2 AS ( SELECT * FROM Cte2 ORDER BY Number DESC )
SELECT * FROM Name1
UNION ALL
SELECT * FROM Name2;

Recursive CTEs

Recursive CTEs are explained in this blog post "https://bizkapish.com/monetdb/0510-jdbc-recursive-ctes-new-functions-in-monetdb/".

0180 SQL Merge in MonetDB

MonetDB / By / November 9, 2025

Introduction

Merge is used when we want to use records from one table to decide what records to modify in another table. Let's assume that we want to keep two tables synchronized. In that case, every change on the first table should be reflected on the second table.

For full reflection, all of the updates, deletes or inserts that are done on the A table should also be done on the B table.

For partial reflection, we can do just the part of the full reflection. For example, new rows from the A table will also be added to the B table. Records updated or deleted in the table A, will not be updated or deleted in the table B.

Merge statement can not do the full reflection, but it can do partial reflections. We will se such examples bellow.

Sample Tables

We will create two tables. We will try to propagate all the changes in the table A to the table B. For start, we will enter two rows in the table A.

CREATE TABLE A ( Letter CHAR, Number INTEGER );
INSERT INTO A ( Letter, Number ) VALUES ( 'A', 1 ), ( 'B', 2 );

CREATE TABLE B ( Letter CHAR, Number INTEGER );

Partial Synchronization

Initial Synchronization with Merge INSERT

All the rows from the table A that do not exist in table B will be inserted into table B.

MERGE INTO B
     USING A
        ON B.Letter = A.Letter
      WHEN NOT MATCHED THEN INSERT ( Letter, Number ) VALUES ( A.Letter, A.Number );		MERGE INTO targetTable
USING sourceTable
ON matchingCondition
WHEN NOT MATCHED THEN INSERT RECORDS

Now, table B, has the same rows as the table A.

Merge with UPDATE

First, we will update the table A. We will change A1 to A4.

UPDATE A SET Number = 4 WHERE Letter = 'A';

Then we'll push that change to the table B. Notice that we don't use 'WHEN NOT MATCHED'. Now we use 'WHEN MATCHED'.

MERGE INTO B     
     USING A        
          ON B.Letter = A.Letter and A.Letter = 'A'
      WHEN MATCHED THEN UPDATE SET Number = A.Number;


Merge with DELETE

We will update one record in the table A.

UPDATE A SET Number = 8 WHERE Letter = 'B';

Now, we will delete all the rows from the table B, that do exist in the table A. Row A4 exists in both tables, so that row will be deleted.
This is not the behavior that we would expect. We are deleting matching rows.

MERGE INTO B
     USING A
        ON B.Letter = A.Letter and B.Number = A.Number
      WHEN MATCHED THEN DELETE;

Merge Matrix

When rows are matched, we can do UPDATE or DELETE.
When rows are not matched, we can do INSERT.
I would expect DELETE to work with "Not matched", but it is not. It works with "Matched".

Complex Merge

The great thing about MERGE statement is because we can do two things in one statement. We can only do ( INSERT and UPDATE ) or ( INSERT and DELETE ).

Merge with INSERT and UPDATE

This time we will do INSERT and UPDATE at the same time.

MERGE INTO B     
     USING A        
        ON B.Letter = A.Letter      
      WHEN NOT MATCHED THEN INSERT ( Letter, Number )                            
                             VALUES ( A.Letter, A.Number )      
      WHEN MATCHED THEN UPDATE SET Letter = A.Letter,
                                   Number = A.Number;

Merge with INSERT and DELETE

Currently, tables A and B are equal. We will add a row to table A to show how to use merge with INSERT and DELETE.

INSERT INTO A ( Letter, Number ) VALUES ( 'E', 5 );

MERGE INTO B
     USING A        
        ON B.Letter = A.Letter
      WHEN NOT MATCHED THEN INSERT ( Letter, Number )
                            VALUES ( A.Letter, A.Number )
      WHEN MATCHED THEN DELETE;  

Things That Don't Work in Merge

INSERT with Subquery

Subqueries are not supported in INSERT clause, inside of Merge statement.
MERGE INTO B
          USING A
                ON B.Letter = A.Letter
            WHEN NOT MATCHED THEN INSERT SELECT * FROM A;

Several MATCHED, or NOT MATCHED sentences

We can only use one MATCHED clause and/or one NOT MATCHED clause.
MERGE INTO B
     USING A
        ON B.Letter = A.Letter
      WHEN MATCHED THEN DELETE
      WHEN MATCHED THEN UPDATE SET Letter = A.Letter,
                                   Number = A.Number;

Multiple matches

I will add row "E6" in the table "A" with a statement "INSERT INTO A VALUES ( 'E', 6 );". Now this table has rows E5 and E6. If we now apply MERGE statement, both rows E5 and E6 will try to update row E5 in the table B. This is not allowed and will fail.

MERGE INTO B USING A ON B.Letter = A.Letter
WHEN MATCHED THEN UPDATE SET Letter = A.Letter, Number = A.Number;

0170 Sampling, Analyze, Prepare in MonetDB

MonetDB / By / November 7, 2025

Let's create test table:

1) CREATE TABLE samplingTable ( Letter CHAR, Number INTEGER );

2) INSERT INTO samplingTable ( Letter, Number )
  VALUES ( 'A', 1 ), ( 'B', 2 ), ( 'C', 3 ), ( 'D', 4 ), ( 'E', 5 )
, ( 'F', 6 ), ( 'G', 7 ), ( 'H', 8 ), ( 'I', 9 ), ( 'J', 10 );

Two Ways of Sampling

Sampling of records is done with SAMPLE clause. This clause accepts continuous range [0,1) as an argument. Selected number is percent of records that will become part of the sample. It is also possible to select any integer bigger than zero. That number will become number of units in the sample.

SELECT * FROM samplingTable SAMPLE 0.2;  
 --20%       		SELECT * FROM samplingTable SAMPLE 3;  
--3 units		SELECT * FROM samplingTable SAMPLE 1;       
--1 unit

It is possible to sample from a subquery.
SELECT * FROM
( SELECT * FROM samplingTable SAMPLE 0.1 ) subqueryAlias;
It is possible to use sample in an INSERT statement.
INSERT INTO samplingTable
SELECT * FROM samplingTable SAMPLE 2;

Samples have uniform distribution.

Table Statistics

Statistics System Table

Statistics about tables is placed in the table sys.statistics. In order to read from this system table, we have to log in as an administrator monetdb.
First, we quit current session (1). Then we have to log in as a monetdb (2). Password is "monetdb" (3). Then, we are allowed to read from statistics table (4).

These are the columns in that table:

column_idschematablecolumntypewidthcountuniquenilsminvalmaxvalsortedrevsorted
INTEGERVARCHARVARCHARVARCHARVARCHARINTEGERBIGINTBOOLEANBOOLEANCLOBCLOBBOOLEANBOOLEAN
Internal
ID of column.		Schema name.Table name.Column name.Data
type of column.		Number of bytes.Number
or rows, approximate.		Are values unique in column.True, if there are nulls in column.Minimum in the column or null.Maximum in the column or null.Column sorted ascending.Column sorted descending.

All the strings from this table are small case. When we refer to them, we have to write them exactly like in the table.

SELECT * FROM sys.statistics WHERE COLUMN = 'Letter';This will fail because we have to use lower letters for 'letter'.

Table Producing Functions

Table sys.statistics will give us statistics about all of the user tables in our schema. If we want to read statistics of system tables too, then we should use this table producing function.

SELECT * FROM
sys.statistics();

For reading statistics for one schema, table, or column, we can filter sys.statistics or sys.statistics() tables. Instead of filtering, we should use these table producing functions with arguments which define what data we want to read. This table producing functions are fastest way to get specific statistics.

SELECT * FROM sys.statistics('voc');
Statistics for a schema.		SELECT * FROM
sys.statistics( 'voc','samplingtable');
Arguments are case sensitive. Statistics for a table.		SELECT FROM
sys.statistics('voc','samplingtable','letter');
Statistics for a column.

Refreshing Statistics

We can refresh statistics for the whole schema, for the one table, or for the one column. The refresh will take a long time if we have a lot of data.

ANALYZE voc;  --whole schemaANALYZE voc.samplingtable;     --one tableANALYZE voc.samplingtable ( letter );    --one column

Statistics is used by MonetDB, to optimize queries. If we made a lot of deletes, inserts or updates, statistics will become obsolete so we should refresh it. This will make our queries performant again.

Prepare Statement

If we want to use some statement many times, we can prepare it as well. That means that executing plan for that statement will be cached during the session. Each sequential call of that statement will use cached version, but with different parameters.

As a monetdb user, our default schema is sys. Before going through example, we will first change our current schema to voc.

Now, instead of voc.samplingTable, we can just type samplingTable.

For example, let's say that we want to insert three rows in our table samplingTable. For that we can use three separate statements.

INSERT INTO samplingTable ( Letter, Number ) VALUES ( 'O', 100 );
INSERT INTO samplingTable ( Letter, Number ) VALUES ( 'P', 101 );
INSERT INTO samplingTable ( Letter, Number ) VALUES ( 'Q', 102 );

For each of these statements, MonetDB will create separate execution plan. To avoid doing the same work three times, we will prepare this statement.

Instead of parameters, we will use question marks. They are placeholders for real values.
PREPARE INSERT INTO samplingTable ( Letter, Number ) VALUES ( ?, ? );

Zero, from the image on the right, is an ID of our prepared statement. We can use that ID to call our prepared statement.

We will now execute our three statements from above, by using this prepared statement. Zero is ID of our prepared statement.

EXECUTE 0( '0', 100);
EXECUTE 0( 'P', 101);
EXECUTE 0( 'Q', 102);		This will insert three new rows in samplingTable.

Data about our prepared statements is in the system table sys.prepared_statements.

We can release this prepared statement from our session cache.

DEALLOCATE PREPARE 0;                         --This will remove just prepared statement with ID 0.
DEALLOCATE PREPARE ALL;                     --This will remove all prepared statements.

Prepared statements will be deleted automatically, if any error happens during the user session. If the error doesn't occur and we do not use "DEALLOCATE" then the prepare statements will all be deleted when we exit the session.