0510 JDBC, Recursive CTEs, New Functions in MonetDB     

We will continue using the green and blue server that we have created in this post => link ( or you can watch the video on the youtube  => link ). This was the post about distributed query processing.

monetdbd start /home/sima/monetdb/DBfarmG mclient -u monetdb -d DatabaseG   –password monetdb monetdbd start /home/sima/monetdb/DBfarmB mclient -u monetdb -d DatabaseB   –password monetdb

JDBC

We will now connect to the blue MonetDB server, from the green server, through JDBC connector.

Installing Java

Let's see if we have Java installed. java -version
We don't have it, so we can install it like this: sudo apt install default-jre

Connecting With the JDBC Client

From this link: https://www.monetdb.org/downloads/Java/

Download this file "jdbcclient.jre8.jar".

This is JAR file that includes java console client application, but also the driver. It is all in one.

Inside of the green server, run this command from the shell: java -jar /home/sima/Desktop/jdbcclient.jre8.jar -h 192.168.100.146 -p 50000 -u monetdb -d DatabaseB

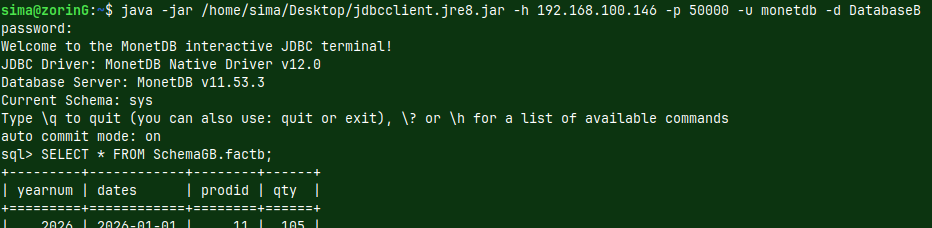We are now connected. We can use this java client at the same way as we use "mclient" program. SELECT * FROM SchemaGB.factB;

Using JDBC Connection with DBeaver

From this link: https://www.monetdb.org/downloads/Java/

Download JDBC driver "monetdb-jdbc-12.0.jre8.jar".

We don't have DBeaver on the green server, so we have to install it. We will download DBeaver ".deb" file with wget command. Then we can install it.

cd /home/sima/Desktop wget https://dbeaver.io/files/dbeaver-ce_latest_amd64.deb sudo apt install ./dbeaver-ce_latest_amd64.deb

DBeaver is a GUI program. Click on Database > Driver Manager menu.

Click "New".

In the new dialog enter these values in "Settings" tab: Driver Name:        MonetDB_JDBC Class Name:        org.monetdb.jdbc.MonetDriver URL Template:     jdbc:monetdb://{host}:{port}/{database}

This is how "Settings" tab should look: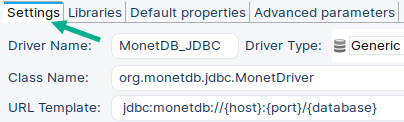

In the "Libraries" tab click on "Add File". Find "monetdb-jdbc-12.0.jre8.jar" driver file. This will add our driver file into DBeaver.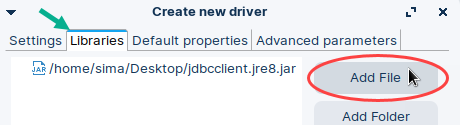

Close everything and in the main window click on the icon for the New Connection.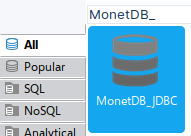

Find our driver with a search. Click Next and in the new dialog enter these values:

Host:                192.168.100.146 Port:                50000 Database/Schema:     DatabaseB Username:            monetdb Password:            monetdb

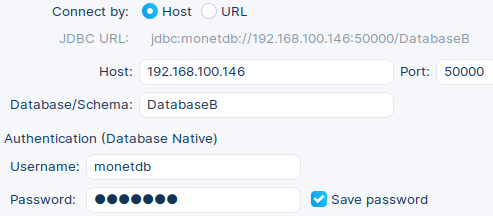This is how dialog will look like. When you click on the "Test" button you will get an error: Invalid JDBC URL:  jdbc:monetdb://192.168.100.146:50000/DatabaseB

This error is because DBeaver is trying to validate "jdbc:monetdb://192.168.100.146:50000/DatabaseB" URL, or it is trying to add some hidden parameters or escape characters.

Solution is to change dialog to manual input.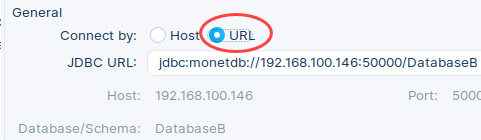

DBeaver will now use the raw URL. After we click on the "Test" button, we will get confirmation dialog.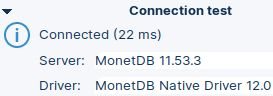

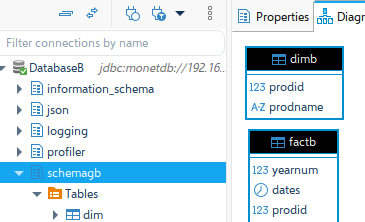We can now expand our connection and there we will find all of the schemas and tables, and now we can run queries.

Recursive Common Table Expressions

In the blog post about common table expressions ( link ), I unintentionally lied that MonetDB doesn't support Recursive CTEs. But it does, and I will explain them now.

What is Recursion

When we need to take a shower, it is always difficult to set the right water temperature. To find it, we repeat the same action. We move the lever left and right until we find the perfect spot. With each movement of the lever, we get closer to the desired temperature.

Recursion is an iterative process of finding a solution. We repeat the same logic each time, but each time we are closer to the solution because we can base our logic on the information we have gained during previous iterations.

Let's look at this example. Our friend imagined a number between 1 and 10. We have to guess that number with the minimal number of questions. The best approach is to use binary logic, based on an elimination process where in each iteration we can remove half of the numbers.

Question: Is it bigger than 5?   Answer: Yes, it is.

Question: Is it bigger than 8? Answer: No, it is not.

Question: Is it smaller than 7? Answer: Yes, it is.

It has to be 6.

The only argument in our alghorithm is the range of the possible numbers. Our logic has two steps: 1) Does the range of possible numbers has only one number. 2) If it doesn't, ask the question to eliminate half of the numbers and reduce the range of possible numbers by half.

We can pack the second step into function with a name "EliminateHalf". This function will return the range of all the possible numbers. We will call this function 3 times.

1) EliminateHalf (1,2,3,4,5,6,7,8,9,10) = (6,7,8,9,10) 2) EliminateHalf (6,7,8,9,10) = (6,7) 3) EliminateHalf (6,7) = (6)

We can nest these functions: EliminateHalf(EliminateHalf(    EliminateHalf(         1,2,3,4,5,6,7,8,9,10))) = 6

Problem is that we don't know how many nested functions do we need. I will create a pseudo code that will nest as many functions as needed to get the final result.

Result = EliminateHalf( 1,2,3,4,5,6,7,8,9,10 )  # initial state Do Until Count( Result ) = 1                    # are we finished        Result = EliminateHalf( Result )            # if not, continue  Loop

This is RECURSION. We broke the complex problem into small steps. Each step has the same logic. Each step is using arguments that are the result of the previous step. This is just one iterative process which brings us closer to the solution with each step.

You want example from the real life. The coach of the football team analyze data from the previous game. After each analysis he change the game of his team. He continues with this practice until his team start winning.

The Structure of Recursion

Recursion structure always has four steps. The first step "initial state" is a problem that we want to solve. We will solve it by improving our statistics.

1) Set initial values for our arguments.                                                     # initial state                           2) Has our goal been achieved?                                                                 # are we there yet            # recursive part 3) Improve our arguments by using some strategy.                             # continue with effort     # recursive part 4) Repeat steps 2 and 3 until we reach the goal.                                   # be persistent

Linear and Tree Recursion

In linear recursion we only have two possible outcomes. We are either satisfied with the result or we will continue with our effort. For example, the coach can be satisfied with his team or he can continue introducing improvements.

Tree Recursion is when we have several possible strategies to direct our effort. For example, the coach can change the team's game, or he can look for position in some other team. If we create a diagram of his possible actions we can get something like this:

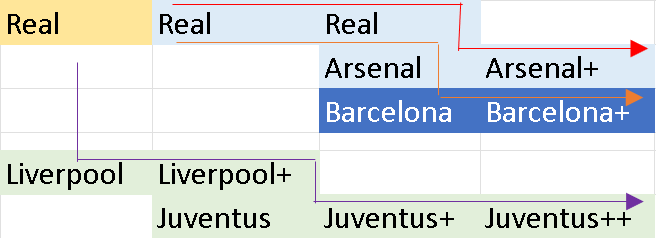1) Red path: Be satisfied with a Real, and then transfer to Arsenal, and start improving Arsenal game. 2) Orange path: Be satisfied with a Real, and then transfer to Arsenal, and then to Barcelona, and start improving Barcelona's game. 3) Purple path: Leave Real, improve Liverpool for a while, and then transfer to Juventus to improve Juventus game.

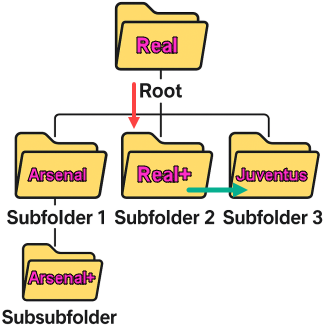We can present this coach career as folders and subfolders. Each time he improves his team, he is going deeper in the subfolders ( Real → Real+ ). Each time he changes his job, he is moving to another folder at the same level ( Real+ → Juventus ). This is why this kind of recursion is called Tree Recursion, because we have a hierarchy. This hierarchy is reflection of strategic decisions we have to make to reach our goal. Each decision will move us to another path, but we always use the same logic to decide.

Structure of The Recursive Common Table Expression

WITH RECURSIVE cte_name AS (     SELECT ...           –initial state     UNION ALL         SELECT ...           –continue with improvements     FROM cte_name        –get the previous state     WHERE ...            –are we there yet ) SELECT * FROM cte_name;  –return result

In the simplest form, recursive CTE has two SELECT statements connected with UNION ALL. First select statement will define initial state. RECURSIVE CTE will return all interim results connected with UNION ALL. Second select statement will calculate the new status. It will reference the previous status by the name of the CTE. WHERE in second select statement will tell us when to stop.

WITH RECURSIVE numbers(n) AS (    SELECT 1           UNION ALL          SELECT n + 1     FROM numbers     WHERE n < 4 ) SELECT * FROM numbers;

The first select statement is called ANCHOR member. The second one is RECURSIVE member. ANCHOR member will be executed only once. In this example, RECURSIVE member will be executed several times, each time with the different value of "n", until the condition becomes false.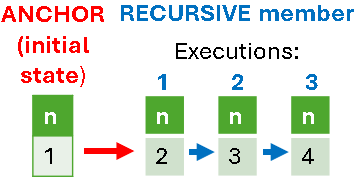

We will apply UNION ALL on all of the interim results.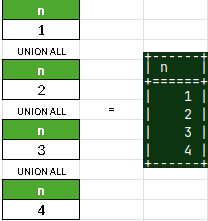

WITH RECURSIVE factorial(n, fact) AS (     SELECT 1, 1           UNION ALL          SELECT n + 1, fact * (n + 1)     FROM factorial     WHERE n < 5 ) SELECT n, fact FROM factorial;

This is an example how to calculate factorial.

These two examples are for the linear recursion.

Tree Recursion

This is our hierarchy.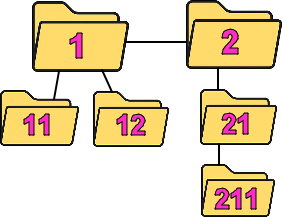

Our hierarchy can be presented with the self referencing table. We'll create such table in MonetDB.

CREATE TABLE Folders ( Folder TEXT, Parent TEXT ); INSERT INTO Folders ( Folder, Parent ) VALUES ('Folder1', NULL), ('Folder2', NULL), ('Folder11', 'Folder1'), ('Folder12', 'Folder1'), ('Folder21', 'Folder2'), ('Folder211', 'Folder21');

We'll make our CTE: WITH RECURSIVE Folder_paths AS (     SELECT Folder, Folder AS Path     FROM Folders     WHERE Parent IS NULL     UNION ALL     SELECT f.Folder, fp.Path || '>' || f.Folder AS Path     FROM Folders f  JOIN Folder_paths fp ON f.Parent = fp.Folder ) SELECT * FROM Folder_paths ORDER BY path;

This is initial state. This table represents folders at the top level.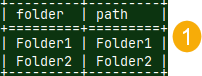 We'll join original Folders table with this initial state. That will give us our new state.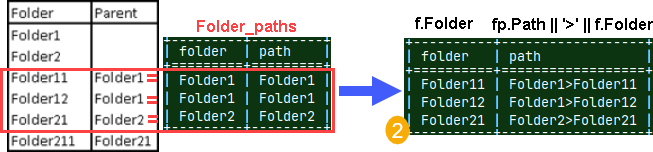

We'll do it again, between Folders table and new state. This is inner join.

We can now make a final result as a union between (1),(2),(3).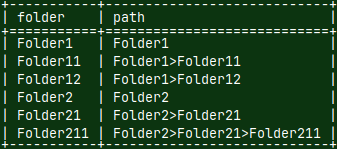

Tree recursion occurs then ANCHOR and RECURSIVE members are select statements that return tables with several rows. Those rows represent folders at the same level. We have (1), (2), (3) for top (1), middle (2) and bottom (3) folders. First, we get top folders (initial state), then middle folders (first recursion), and then bottom folders (second recursion). Each recursion is used to collect folders from the level bellow.

Recursive CTEs Caveats

1) Recursive and anchor member must match in columns number and data types.

2) If we use UNION ( instead UNION ALL ), recursion will stop immediately when we face a duplicate. This statement  will immediately end, although it doesn't have WHERE statement. This is because the first recursion will return number 1, which is a duplicate. UNION operator will remove that duplicate, so our result will have only one row, and that row will have the original number 1.

WITH RECURSIVE numbers AS (     SELECT 1     UNION     SELECT 1 FROM numbers ) SELECT * FROM numbers;

3) Don't user OUTER JOINS in the recursive member. The query will never end. Only INNER join is acceptable.

4) MonetDB will not complain if we use aggregate or window functions in recursive member. We can also use DISTINCT and GROUP BY in the recursive member. In MonetDB, we can use CTE's name in the FROM clause, but we can also use it in subquery. Some other servers don't allow this.

New Functions

DayName and MonthName Functions

SELECT DAYNAME('2025-07-12');	Saturday	This function returns a name of a day in a week according to the current locale, set in the OS.
SELECT MONTHNAME('2025-07-12');	July	This is similar function that is returning the name of a month.

Beside date arguments, we can also use timestamp ('1987-09-23 11:40') or timestamp TZ ('15:35:02.002345+01:00').

Generate Series Functions

SELECT * FROM generate_series(1,9,2);

1,3,5,7

This function will return numbers from 1 do 9, with step 2. Default step is 1.

SELECT * FROM generate_series('2025-01-01','2025-01-10',INTERVAL '5' DAY);	2025-01-01,2025-01-06	All dates from the range, but with the step of 5 days.
SELECT * FROM generate_series('2025-01-01','2025-05-10',INTERVAL '2' MONTH);	2025-01-01, 2025-03-01	We can also get the months with the step od 2 months.

We can list seconds or days between two timestamps.
SELECT * FROM generate_series('2025-01-01 01:40:00','2025-01-01 1:40:05', INTERVAL '3' SECOND);	2025-01-01 01:40:00 2025-01-01 01:40:03
SELECT * FROM generate_series('2025-01-01 01:40:00','2025-01-06 1:40:05', INTERVAL '3' DAY);	2025-01-01 01:40:00 2025-01-04 01:40:00

Generate Series functions will return a column with the name "value". SELECT * FROM generate_series( 1,7,2); 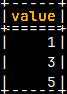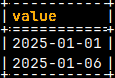SELECT * FROM generate_series('2025-01-01','2025-01-10',INTERVAL '5' DAY);

---